Need help choosing the right product?
Our tool will match the best product to your needs
Launch product selectorWelcome to the Global Website
We have detected that you may prefer the Global site. Please use the language dropdown above to change your selection if required.
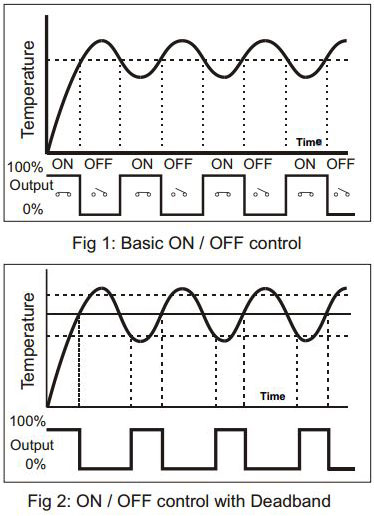
On / Off control is the simplest means of control but gives rise to fluctuations in the process variable (Fig 1). A degree of hysteresis or deadband must be set in On / Off control if the operation of the switching device is to be reduced and relay chatter is to be avoided (Fig 2).
On / Off control is a very simple form of control, which leads to oscillation of the process variable. This oscillation can affect the quality of the final product and is undesirable. The alternative is to use three term control, known as PID control.
To find out which temperature controller best fits your needs:
A ‘ closed loop ‘ consists of :

Simple On/Off control could be thought of as starting the engine (G(s)) of the car (Plant), pressing the accelerator (Output) to the floor until the desired speed (SP) of 80 kph is reached as indicated on the speedometer (PV), then taking your foot completely off the accelerator. When the speed drops below 80 kph the accelerator is again depressed to the floor until 80 kph is again reached.
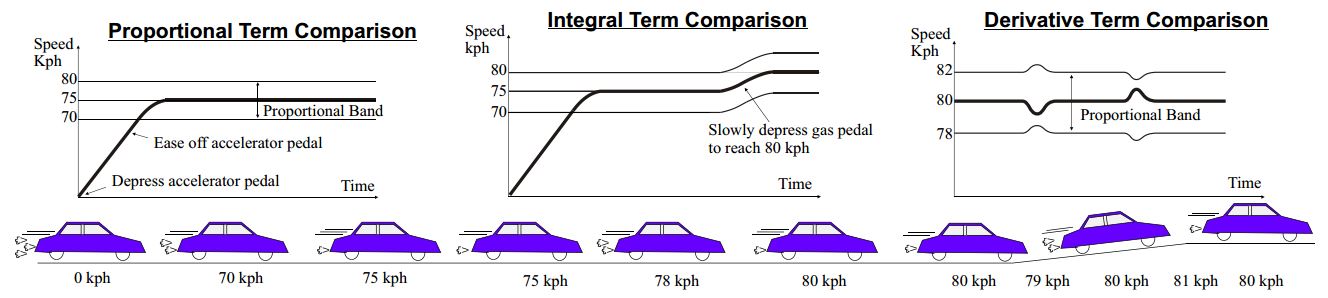
Comparison to the Proportional Term
If we wish to drive from a standstill to 80 kph we can consider the procedure we adopt to achieve this to explain the Proportional term.
From a standstill we depress the accelerator pedal. The speed of the vehicle will increase and at a certain speed below our target speed of 80 kph we begin to ease off the accelerator pedal in order to prevent cruising past the desired speed. This easing off the accelerator pedal can be directly compared to entering the Proportional Band or the band relative to the required speed. If we do not look at the speedometer we will certainly drive at a speed that is not our desired speed and an error will result.
Comparison to the Integral Term
If we now look at the speedometer we see that we are low of our desired speed and using this visual feedback we correct for the error and begin to slowly depress the accelerator pedal. As a result our speed slowly increases to achieve the desired speed of 80 kph.
This procedure can be compared to the Integral Time of a PID controller.
Comparison to the Derivative Term
We are now cruising at our Setpoint of 80 kph and we continue to maintain this speed through visual feedback of the speedometer.
If we encounter a sudden change in slope of the road such as a hill we correct for the reduction in speed which would result by depressing the accelerator pedal more than would otherwise be the case for the slight reduction in speed we initially encounter. As the slope of the road levels off again we ease off the accelerator pedal more than would otherwise be the case for the slight increase in speed to avoid raising our speed too far beyond our target speed.
The amount of correction and time to reduce this correction to zero can be compared to the Derivative Time.
When we have driven a car for some time these procedures become second nature to us and we do not think about the technique we use to drive. Consider, however, the process of someone learning to drive and you will observe these descriptions in action.
Different process variables such as temperature, speed, pressure etc. all have different characteristics. For example a temperature on an extruder barrel responds very slowly whereas the speed responds much more quickly and the pressure can respond more quickly still.
The information given above may make it appear easy to generate a PID controller using simple mathematical terms. In reality, industrial control manufacturers develop sophisticated control algorithms, containing many other features than those described above. In this way they are able to provide the industry with controllers which give excellent performance in a wide range of control applications.
Additional techniques are also included to prevent the Integral term from saturating during open loop conditions and to prevent overshoot of the Setpoint value. The two conditions of start-up or changed setpoint and normal running conditions generally require different responses. Advanced control algorithms are developed by control companies to compensate for both conditions.
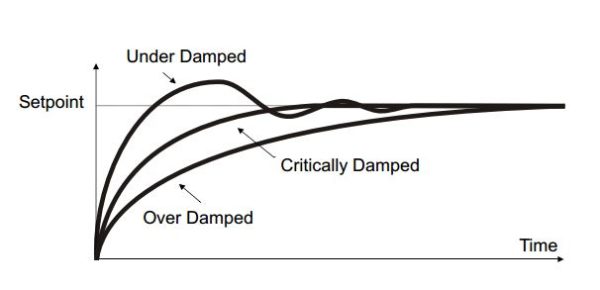
The combination of the three terms can provide a stabilizing effect on a process only if the terms are correctly set. This is referred to as ‘ tuning the loop ‘. If we ignore the situation of loop oscillation, there are three categories of loop performance :
Under Damped
In this situation the terms are set to prevent oscillation but do lead to an overshoot of the Process Value followed by decaying oscillation to finally settle at the Setpoint. This type of response does give a minimum time to Setpoint but overshoot may cause problems in certain situations and the loop may be sensitive to sudden changes in Process Value. This will result in further decaying oscillations before settling once again.
Critically Damped
This represents and ideal situation where overshoot does not occur and the process responds to changes in a controlled, non oscillatory manner.
Over Damped
In this situation the loop responds in a controlled but sluggish manner which will result in a loop performance which is non ideal and unnecessarily slow. The balancing of the P, I and D terms depends totally upon the nature of the process to be controlled.
In a plastics extrusion example, a barrel zone will have a different response to a casting roll, drive loop, thickness control loop or pressure loop. In order to achieve the best performance from an extrusion line all loop tuning parameters must be set to their optimum values. Needless to say, many extrusion lines and industrial equipment are not set up to give their best performance.
There are many documented methods of tuning a loop with the most common methods being the following:
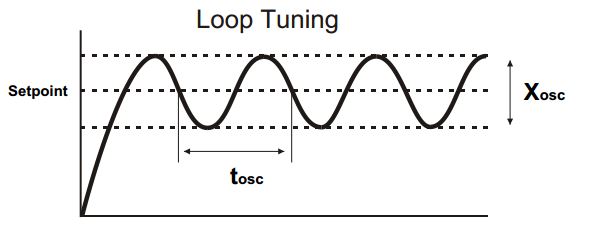
Ziegler Nicholls: This method involves putting the loop into oscillation and measuring the oscillation period T. The oscillation is caused by setting the I and D terms to off and reducing the Proportional Band until the loop just oscillates. The setting of the P term at the onset of oscillation (Px) is used to determine the desired Proportional Band.
Cohen & Coon: In this method power is applied from a low Process Value and a note is made of the time before any response is observed ( dead time ) and the maximum rate of change of the Process Value. By combining this information with the final settling of the Process Value resulting from the power applied, the P, I and D values are calculated.
Popular Method (Rule of Thumb)
An easier method of manually determining the P, I and D values is to set the Integral and Derivative terms to off and to set the Proportional Band to a minimum. The resulting oscillation width Xosc and the oscillation period tosc can be used to determine the PID settings shown below.
P = 2.0 * Xosc
I = 1.5 * tosc
D = I / 5
These values result in a slightly over damped response and consequently all values can be reduced slightly to give a more responsive loop.
Auto Tuning: (Standard with all Eurotherm PID Controllers)
The standard initial method of tuning a process loop is to use the advanced adaptive tuning algorithms inbuilt in today’s controllers, to automatically test the loop and implement the optimum PID control parameters.
Care should be taken to ensure that the oscillations of the Process Value will not damage the process being tuned. It is recommended to set the Setpoint for tuning purposes below the normal running Setpoint value.

Avoiding Overshoot
Various techniques are used to avoid overshoot. The aim is to prevent the process value from exceeding the desired value or setpoint. In the example shown the proportional band is brought down to meet the approaching process value in order to reduce the output power and to smoothly bring the process value to the desired setting.
Product Selector
Our tool will match the best product to your needs
Launch product selectorContact Us